Definition
纠删码是一种系统设计中的数据保护方法，用于确保数据的可靠性和可用性。它通过将数据分割成更小的数据块，并使用数学算法创建额外的数据片段（称为校验数据），从而实现这一功能。这使得系统即使在某些数据块丢失或损坏的情况下也能恢复原始数据。
- 数据分片：原始数据被分割成多个数据块。
- 校验和生成：使用 Reed-Solomon 等算法生成额外的校验和块。
- 存储：数据和校验块被分布到不同的存储节点或设备上。
- 恢复：如果某些数据块丢失或损坏，系统可以使用剩余的数据块和校验数据来重建原始数据。
Reed-Solomon Encoding Matrix Example
数学家们已经几个世纪以来一直在研究矩阵代数、群论和信息论。Reed 和 Solomon 利用这些知识创造了一种看似神奇的编码系统。它可以将信息分解成 n 个部分，添加 k 个“校验”部分，然后从 (n+k) 个部分中的 n 个部分中重建原始信息。
下面的示例使用“4+2”编码系统，其中原始文件被分成四块，然后添加两块校验块。
原始数据
在这个例子中，文件的四个部分每个都是四个字节长。每个部分是矩阵的一行。第一个是“ABCD”。第二个是“EFGH”。以此类推。Reed-Solomon 算法创建一个编码矩阵，你用这个矩阵乘以你的数据矩阵来生成编码数据。该矩阵的设置方式是，结果的前四行与输入的前四行相同。这意味着数据保持完整，它实际上只是在计算校验位。
应用编码矩阵
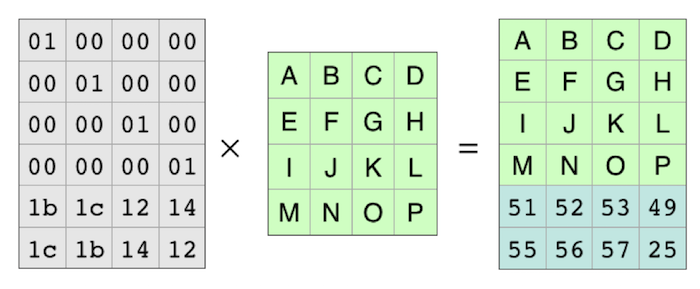
结果是比原始矩阵多两行的矩阵。这两行是校验位。
编码矩阵的每一行都会生成结果矩阵的一行。因此编码矩阵的每一行都会生成文件结果的一部分。由于行是独立的，你可以划掉两行，方程仍然成立。
数据丢失：六行中有两行“丢失”
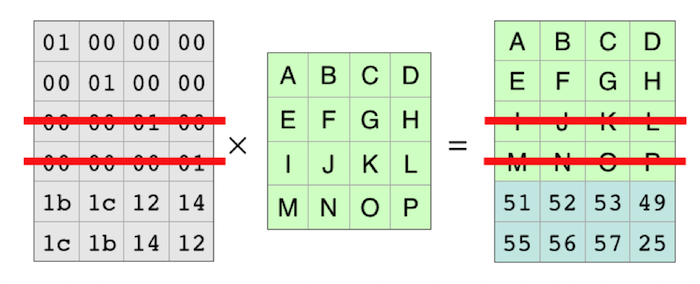
那些行完全消失后，看起来是这样的：
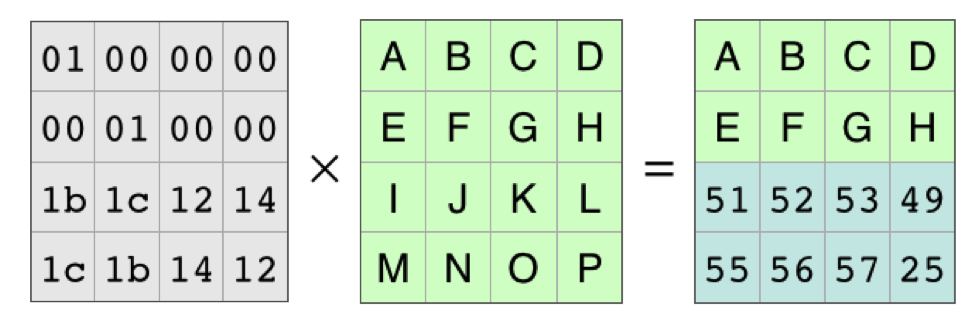
由于数学家多年来所做的所有工作，我们知道编码矩阵，即左侧的矩阵，是可逆的。存在一个逆矩阵，当它与编码矩阵相乘时，会产生单位矩阵。就像在基础代数中一样，在矩阵代数中你可以用相同的东西乘以等式的两边。在这种情况下，我们将用单位矩阵从左侧进行相乘：
将方程两边乘以逆矩阵
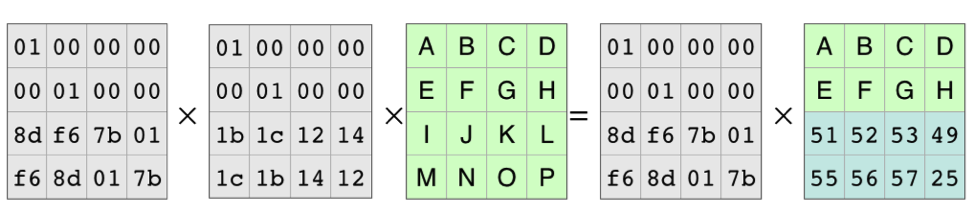逆矩阵和编码矩阵相互抵消
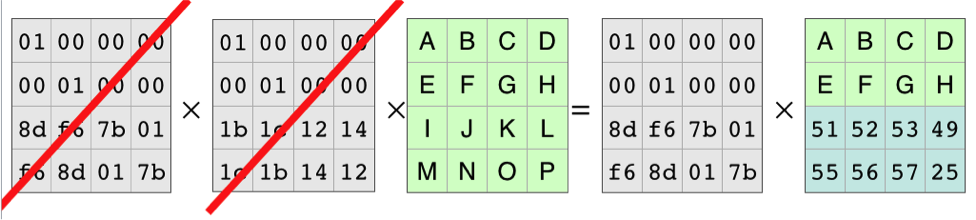
重建原始数据
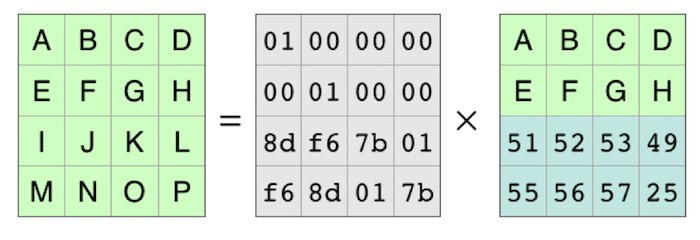
因此，要制作解码矩阵，过程是取原始编码矩阵，划去缺失部分的行，然后找到逆矩阵。接着，你可以将逆矩阵与可用的数据部分相乘，以重建原始数据。
Reference
1.Backblaze Open-sources Reed-Solomon Erasure Coding Source Code
2.Erasure Coding in System Design
