Optimization for Unconstrained Differentiable Functions
1.1 Mathematical optimization
$\frac{x ^2}{a^2} + \frac{y ^2}{b^2} = 1$ $\textit{f}_0 =4|x||y|$
A mathematical optimization problem, or just optimization problem, has the form maximize $\textit{f}_0 $
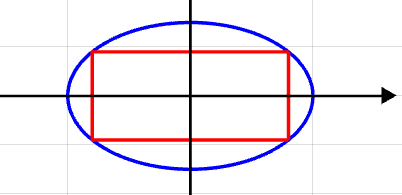
use x to represent $\textit{f}_0 $
$\textit{f}_0 =4xb\sqrt{1-\frac{x^2}{a^2}} $
$x>0$
we need to make $\textit{f’}_0 =4b \left( \sqrt{1 - \frac{x^2}{a^2}} - \frac{x^2}{a^2 \sqrt{1 - \frac{x^2}{a^2}}} \right)=0$
$ x=\frac{\sqrt2a}{2}$
find out the max of $\textit{f}_0$ is $2ab$
1.2 Gradient descent
Let’s try to find the minimum value of
$\textit{f}(x,y) = x^3-y^3+3x^2-3y^2-9x$
begin point: $\textit{x}_0=3,\textit{y}_0=3$
1.Gradient Descent
First,calculate the gradient,
$\nabla \textit{f}_{(x,y)}=(\frac{\partial f}{\partial x },\frac{\partial f}{\partial y }) $
$\frac{\partial f}{\partial x }=3x^2+6x-9$
$\frac{\partial f}{\partial y }=-3y^2-6y$
Second,select a suitable learning rate , we try to set $\alpha =0.01$,which can be changed if not suitable.
Iterative updates:
$x_{n+1}=x_{n}-\alpha \frac{\partial f}{\partial x }$
$y_{n+1}=y_{n}-\alpha \frac{\partial f}{\partial y }$
Ending up finding the minimum value $f_{(1,-2)}=-9$
2.Hessian Matrix and Extreme Value Discrimination Method
$f_{(x,y)}$ is at the critical point $(a,b) \iff \frac{\partial f}{\partial x }=0,\frac{\partial f}{\partial y }=0$ Hessian matrix is
$ H=\begin{vmatrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial f^2}{\partial x \partial y} \newline \frac{\partial f^2}{\partial x \partial y} & \frac{\partial^2 f}{\partial x^2} \end{vmatrix} $
If the second-order partial derivatives are continuous,$\frac{\partial f^2}{\partial x \partial y}=\frac{\partial f^2}{\partial y \partial x}$ Discriminant: $D=\frac{\partial^2 f}{\partial x^2}\frac{\partial^2 f}{\partial y^2}-(\frac{\partial f^2}{\partial x \partial y})^2$
- $D>0,\frac{\partial^2 f}{\partial x^2}>0 \to $ mininmum value point
- $D>0,\frac{\partial^2 f}{\partial x^2}<0 \to $ maxinmum value point
- $D<0 \to $ saddle point (non-extremum)
- $D=0 \to$ cannot determine (requires further analysis)
To sum,gradient descent normally use $x_{n+1}=x_{n}-\alpha Grad(\textit f_{(x)})$
1.3 Newton method
I $ x_{n+1}=x_{n}- \frac {\textit f(x_{n})}{\textit f’(x_{n})} $
Geometric intuitive derivation:
At point $x_{n}$,draw the tangent line of the function $y=f(x)$,the intersection point of this tangent line with the x-axis is used as the next estimate.
$y -f(x_{n})=f’(x_{n})(x-x_{n})$,
$0 -f(x_{n})=f’(x_{n})(x-x_{n})$,
$\to x_{n+1}=x_{n}- \frac {\textit f(x_{n})}{\textit f’(x_{n})}$
II $ x_{n+1}=x_{n}- \frac {\textit f’(x_{n})}{\textit f’‘(x_{n})} $
Taylor expansion:
$f(x_{k}+t) \approx f(x_{k})+f’(x_{k})+ \frac {1}{2}f’‘(x_{k})t^2$,
$\frac {\partial f(x_{k}+t)}{\partial t} \approx f’(x_{k})+f’‘(x_{k})t=0 \to t=- \frac {\textit f’(x_{n})}{\textit f’‘(x_{n})}$,
$x_{n+1}=x_{n}- \frac {\textit f’(x_{n})}{\textit f’‘(x_{n})} $