Lecture 1: Unconstrained Optimization for Differentiable Functions

几个无限制可微问题的优化：

对于一般的函数求极值问题：

• 一个变量的函数可以求导，极值一般在导函数的零点。 如：求极小值$f(x)=x^2-1$
• 多个变量的函数可以求偏导，极值一般在偏导函数的零点。 如：求极值$f(x,y)=x^3-y^3+3x^2+3y^2-9x$ 对得到的四个驻点进行的二阶导数检验（Hessian 判别法）

令$a=f_{xx}$

1
2
3
4
5
6
7
    若 ∣H∣>0且 a>0 → 局部极小值（Ext. small）

    若 ∣H∣>0 且 a<0 → 局部极大值（Ext. large）

    若 ∣H∣<0 → 鞍点（uncertain，即非极值点）

    若 ∣H∣=0 → 无法判断（需要更高阶检验）

梯度下降求极大/极小值：

对一个复杂的函数求极值是一件困难的事，梯度下降可以使它变得简单。

$\implies x=x_0-\Delta x$

设置一个学习率a,或者叫步长，

$\Delta x=a f’(x_0)$

然后就是一个迭代的过程：

$x_{k+1}=x_k-\Delta x_k$

$f’(x_k)=0$时到达极值点。

牛顿法-I解决等式限制的优化：

思想也是迭代。

如：$e^x-2x^2+3x-4=0$

迭代$(x_n,f(x_n))$

${y=f’(x_n)(x-x_n)+f(x_n)} \xrightarrow {\text{y → 0}}{x=x_n-\frac{f(x_n)}{f’(x_n)}}$

所以：

$x_{k+1}=x_k-\frac{f(x_k)}{f’(x_k)}$

当$f’(x_k) or f(x_k) $接近0时，停止迭代。

牛顿法-II解决求极小值优化：

定义$f(x),x_k,t$,t是一个很小的数。

泰勒展开：

$f(x_k+t)=f(x_k)+t f’(x_k)+f’‘(x_k)(t^2)$

对t求导：

$f’(x_k+t)=f’(x_k)+t f’‘(x_k)$

$t=-f’(x_k)/f’‘(x_k)$

故迭代：

$x_{k+1}=x_0$

$x_{k+1}=x_k+t$

Lecture 2: Introduction to Linear Programing

线性规划的问题

一般的，线性规划问题包含目的，也就是求最大值还是最小值，

约束条件，也就是变量的取值范围，

目标函数，也就是变量的取值。

如：

$max. f(x)$

$s.t. Ax=b$

$x \in R^n$

建立了类似上面的模型之后，我们可以用线性规划的方法来求解。有可行解时，可行解域常常是一个凸集，最优解在可行解域的边界上（顶点）。

线性规划的数值解

• In the year of 1939, L. Kantorovich proposed LP

• In the year of 1947, G. Danzig invented “Simplex” method

• In the year of 1944, John V. Neumann proposed game theory

• In 1984, Narendra Karmarkar proposed “inner-point” method of LP

• “Inner-point” guarantees to solve LP in polynomial time complexity

LP问题在$s.t. Ax \leq b$时，可以引入松弛变量使得形如$s.t. Ax+S=b$

Lecture 3: Simplex Method

用单纯形表解线性规划

通常给定形式如下：

$max. f(x)$

$s.t. Ax \leq b$

$x \geq 0$

我们可以将其转化为标准形式：

$max. Z= f(x)$

$s.t. Ax+S=b$

$x \geq 0$

然后我们可以用单纯形表来求解。

$Z- f(x)=0$

$s.t. Ax+S=b$

$x \geq 0，s \geq 0$

1.选择在目标函数行（第 0 行）中，系数最负的项，作为入基变量。

2.选择在约束条件列中，解最小的项，作为出基变量。

3.将出基变量的系数化为 1，其余列系数化为 0。

4.将目标函数行中，系数最负的项系数化为 0。

5.重复 1-4 步，直到对应于非基变量的底部行（目标函数行，通常标记为’z’）的所有项都是非负的（>=0）。

特殊情况及停止条件：

1.无界解：如果选择一个进入变量（最大化时 z 行中为正，最小化时为负），但该变量在约束行中的所有项为零或负，则问题无界。

2.退化/停滞：可能在非基变量的 z 行中有一个零，但无法进行出基操作（离开变量的正比没有正值）。这并不总是最终停止的信号，但可能表示存在替代最优解或潜在的循环。

3.本质上，只要能够改进目标函数，就继续出基操作；一旦无法改进，就找到了最优解（或无界条件）。

收敛和复杂度

如果单纯形法是非退化的（预期），顶点数量有限，那么最终会收敛到一个最优解。

但是，给定一个线性规划问题，令有n个变量，m个约束条件，从m个约束条件中选择n个来求一个基本解

$A \subset R^{m \times n},m \leq n$

在寻找基本解时，我们会从 n 列中选出 m 列，构成一个 m×m 的非奇异矩阵 B，这 m 列对应的变量叫做基变量，其他变量设为 0，解得到一组基变量的值，这组解称为一个基本解（如果满足非负约束，就是基本可行解）。

选择基变量就是选择 m 个列（从 n 列中选出），所以可能的基的数目为组合数：

$\begin{pmatrix} n \newline m \end{pmatrix}$=$\frac{n!}{m!(n-m)!}$

这个数字可能会很大，所以单纯形法的复杂度是指数级别的。

矩阵操作的单纯形法

大的LP问题应该用矩阵操作的单纯形法来求解。

核心思想就是将变量分为基变量和非基变量，从而得到基矩阵和非基矩阵，然后用基矩阵的逆来求解非基变量的值，从而得到基本解。在基本解的基础上，我们可以通过矩阵操作来得到更优的基本解，直到基本解的非基变量的值都为非负，具体而言，通过对变量进行出基入基让基本解加的值尽可能大。

Lecture 4: Two-Phase Method, Duality for LP

两阶段单纯形法

引入人工变量和松弛变量，一阶段问题是一个单纯形问题，二阶段问题是一个单纯形问题。

原问题的目标函数是：

$max. Z= f(x)$

$s.t. A_1 x \leq b$

$A_nx \geq b$

$x \geq 0$

引入人工变量和松弛变量，

$max. Z= f(x)$

$s.t. A_1 x +S_1= b$

…

$A_nx -S_n+a_n= b$

$x \geq 0，s \geq 0, a \geq0$

一阶段问题的目标函数是：

$min. z’=\sum_{i=1}^{n} a_i \ or\ max. z’=-\sum_{i=1}^{n} a_i$

$s.t. A_1 x +S_1= b$

…

$A_nx -S_n+a_n= b$

$x \geq 0，s \geq 0, a \geq0$

消掉$a_i$,继续使用单纯形法求解。

如果最小z’=0，那么原问题有解，否则原问题无解。第二阶段则使用第一阶段得到的可行解和原始目标函数来找到原始问题的实际最优解。

二阶段问题的目标函数是：

$max. Z= f(x)$

$s.t. Ax+S=b$

$x \geq 0，s \geq 0$

可以证明：一阶段最优解为0$\iff$原问题有可行解

保持基变量在目标函数行系数为 0

两阶段单纯形法的矩阵操作

与前一步类似

无解和无界的问题

无解：不能找到一阶段最优解为0

无界：

1. 存在一个变量在目标函数行系数为正，但是在约束行中所有项都为零或负

2. 存在一个变量在目标函数行系数为负，但是在约束行中所有项都为零或正

退化线性规划

如果有一个基变量为0，LP问题可能会退化

线性规划中的对偶

求max与求min是等价的，原计算矩阵转置即可

网格最大流问题

一条路径上的最小流量就是这条路径的最大流

Lecture 5: Introduction to QP and Convex Set

例子

一段绳子，长度为8，分成3段，每段围成一个圆形，求最小面积和，

更一般的，

定义lagrange函数 $L(x,\lambda)=x^THx+c^Tx+\lambda(Ax-b)$ 对x，$\lambda$求导

这两个方程就是原问题的约束条件，一般用拉格朗日乘子法来求解

二次规划问题：

• 目标函数是二次函数

• 约束条件是线性函数

Define Lagrangian function

$L(x,\lambda,\beta)=x^THx+c^Tx+\lambda(Ax-b)+\beta(x-0)$

This problem cannot be solved in the analytic way

凸集

凸集定义：

如果对于所有的x,y$\in C$，都有$0 \leq \alpha \leq 1$，都有$\alpha x+(1-\alpha)y \in C$，那么C就是一个凸集。

可以进行相关的灵活证明。

凸包定义：

对于一个集合C，它的凸包就是所有包含C的凸集的交集。

保持集合凸性的操作

1. 凸集的凸包是凸集

2. 凸集的交集也是凸集

3. 凸集的并集也是凸集

证明时想办法将一个集合变成凸集，依靠上面的操作。

Lecture 6: Convex Fucntions

凸函数的定义

对于一个函数$f(x)$，如果对于所有的x,y$\in C$，都有$f(\alpha x+(1-\alpha)y) \leq \alpha f(x)+(1-\alpha)f(y)$，那么$f(x)$就是一个凸函数。对应的，有凹函数（concave）。

函数可微，函数是凸函数$\iff$函数定义域是凸集，$\forall x,y\in R^n,f(y)\geq f(x)+\nabla f^T(x)(y-x)$

可以借助导数的定义证明上面的充分必要

凸函数

定义域是凸集时，P是半正定矩阵 $\iff$ f(x)是凸函数

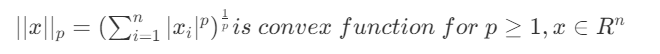
变换保持凸性

积分、仿射变换、指数变换、对数变换、幂次变换，可以使用求导证明凸性。

共轭函数：$f^*(y)=sup_{x\in domf}(y^Tx-f(x))$

原函数是否凸决定于共轭函数是否凸。

求上确界$f^*(y)$：

$f(x)=x^2$

对x求导：

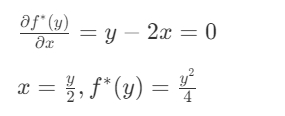
维持函数凸性的同时扩展

将定义域之外的函数值设为+∞。

Lecture 7: Convex Problems

优化问题是凸问题的定义：

• 目标函数是凸函数

• 约束条件是凸函数

• 定义域是凸集

Lecture 8: Lagrangian Multiplier

拉格朗日算子：适用非凸优化、非线性优化、非二次优化

例子

\(\min_{\substack{x_1, x_2 }} \left( x_1 + x_2 \right)\\ s.t. x_1^2 + x_2^2 -1\leq 0\\ \Downarrow \\ \min_{\substack{x_1, x_2 }} \left( x_1 + x_2 +P(x_1^2 + x_2^2 -1) \right)\) 如果x1,x2超出限制，就赋给P一个大值。单纯的大值不可微，所以可以用拉格朗日算子。

$P(y)=\lambda y$ 原例可转化为： \(\underset{x_1, x_2}{\text{Min.}} \, x_1 + x_2 + \underset{\lambda \geq 0}{\text{Max.}} \, \lambda(x_1^2 + x_2^2 - 1)\\ \Downarrow \\ \underset{\lambda \geq 0}{\text{Max.}} \,\underset{x_1, x_2}{\text{Min.}} \, x_1 + x_2 + \lambda(x_1^2 + x_2^2 - 1)\\ \Downarrow \\\) max和min可以交换计算的先后顺序，不影响。之后就是求导计算。

拉格朗日算子

中心思想是将约束条件转化为目标函数的一部分，然后对目标函数求导。 \(\begin{align} \begin{split} &\text{Max. } f(x,y,z) = 4y - 2z \\ &\text{s.t. } \begin{cases} 2x - y - z = 1\\ x^2 + y^2 = 1 \end{cases}\\ &\Rightarrow \\ &\begin{cases} g(x,y,z) = 2x - y - z - 1 = 0\\ h(x,y,z) = x^2 + y^2 - 1 = 0 \end{cases}\\ &\Rightarrow \\ &L(x,y,z) = f(x,y,z) + \lambda g(x,y,z) + \mu h(x,y,z) \end{split} \end{align}\)

Take partial derivative on $x$, $y$, $z$, $\lambda$, $\mu$,

So, maximize of $f$ is $2\sqrt{13} + 2$.

Lecture 9: Lagrangian Dual and KKT Condition

lagrange原问题：

最优解为$p^*$

拉格朗日对偶定义为G：

最优解为$d^*$

$p* \geq d^*$

例子

\(lagrange\ function: L(x,\lambda,\mu)=c^Tx+\lambda(Ax-b)-\mu x\\ =-b^T\mu+(c+A^T\lambda-\mu)^Tx\\ \Downarrow\\ G(\lambda,\mu) =\inf_{\substack{x}}L(x,\lambda,\mu)= \left\{ \begin{aligned} & -b^T\mu & \text{if } A^T\mu-\lambda+c \\ & -\infty & \text{if } x = 0 \\ \end{aligned} \right.\\ p^* \geq d^* =-b^T\mu \ if \ A^T+v \succeq 0\)

KKT条件

• 原问题的最优解是对偶问题的可行解
• 原问题的可行解是对偶问题的最优解 \(L(\lambda, \mu) = f(x) + \sum_{i=1}^{m} \lambda_i g_i(x) + \sum_{j=1}^{p} \mu_j h_j(x)\)

是上问题的最优解

有

Lecture 10: Interior Point Method

Lecture 11: Portfolio Problem

Lecture 12: Support Vector Machine

1. SVM定义

• 一种监督学习分类模型，用于解决二分类问题
• 目标是找到一个超平面，将两类数据分开，且间隔最大

2. 核心思想是最大化间隔

函数间隔定义：

几何间隔：

目标函数：

\(\max_{w,b} \min_{i=1,\ldots,m} r^{(i)}\)

3. 模型建立过程

原始优化问题：

\(\begin{aligned} \max_{w,b,\gamma} &\quad \gamma \\ \text{s.t.} &\quad y^{(i)}(w^T x^{(i)} + b) \geq \gamma, \quad i = 1,\ldots,m \\ &\quad \|w\|_2 = 1 \end{aligned}\)

转化为等价的凸优化问题：

\(\begin{aligned} \min_{w,b} &\quad \frac{1}{2} \|w\|^2 \\ \text{s.t.} &\quad y^{(i)}(w^T x^{(i)} + b) \geq 1, \quad i = 1,\ldots,m \end{aligned}\)

4. 求解方法：拉格朗日对偶

拉格朗日函数：

\(L(w,b,\alpha) = \frac{1}{2} \|w\|^2 - \sum_{i=1}^m \alpha_i \left[y^{(i)}(w^T x^{(i)} + b) - 1\right]\) 其中 \(\alpha_i \geq 0\) 是拉格朗日乘子。

对 (w) 和 (b) 求导：

\(\nabla_w L = w - \sum_{i=1}^m \alpha_i y^{(i)} x^{(i)} = 0 \quad \Rightarrow \quad w = \sum_{i=1}^m \alpha_i y^{(i)} x^{(i)}\)

对偶问题：

将 $ w$ 的表达式代回拉格朗日函数，得到对偶问题： \(\begin{aligned} \max_{\alpha} &\quad G(\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle \\ \text{s.t.} &\quad \alpha_i \geq 0, \quad i = 1,\ldots,m \\ &\quad \sum_{i=1}^m \alpha_i y^{(i)} = 0 \end{aligned}\)

5. 求解与解释

求解方法：

• 常用坐标上升法（Coordinate Ascent）
• 每次更新两个变量 $\alpha_i$ 和 $\alpha_j$

支持向量：

• $\alpha_i > 0$ 对应的样本称为支持向量
• 最终分类超平面由支持向量决定

参数计算：

\(w = \sum_{i=1}^m \alpha_i y^{(i)} x^{(i)}\)

历史

• 提出者：Vladimir Vapnik（1936-）和 Alexey Chervonenkis（1938-2014）
• 地位：深度学习兴起前最流行的分类器

Lecture 13: Integer Programming

整数规划要求解得变量为整数，比LP限制多。

典型问题

• Given variable x1, x2, x3, and x4 ∈ {0, 1}

• The objective is to maximize 8x1 + 11x2 + 6x3 + 4x4

• It is subjective to 5x1 + 7x2 + 4x3 + 3x4 ≤ 14

  剪枝法

  原问题与LP相同，加入整数限制，先按LP计算得到解，IP得到的z值一定不大于LP得到的z值。 选择一个非整数变量（选择最接近x.5的变量）进行向上取整向下取整分情况讨论，对更大的z值进行继续讨论。

  切平面法

  find out the cutting plane, namely the valid inequality. 如果变量非整数，可以加入新的松弛变量对原有的松弛变量约束。

• 选择换出行：右端项为负（最负的）作为换出行
• 选择换入列：选择换入变量时，是用 R0 行的检验数（≥0）除以换出行中负系数的绝对值（或者说除以负数），然后选最小比值（绝对值最小）对应的变量换入。
• 选择换入变量：比值绝对值最小的变量换入

另一种理解：

• 对原问题进行lp求解，在对更接近x.5的变量$x_i$进行分析:

  • 假设原等式： $k_ix_i+a_is_i=\frac{4}{3} $

    分解 $k_i,a_i$ 得到 \(k_i=k_i^*+k_x,0<k_x<1,a_i=a_i^*+a_s,0<a_s<1\)

    得到

    \[k_i^*x_i+a_i^*x_i-1=\frac{1}{3}-k_xs_i-a_sx_s\]

    因为 \(\frac{1}{3}<1,0<a_s<1,0<k_x<1,x_i,s_i\geq 0\\ k_i^*x_i+a_i^*x_i-1 \in I\\ so \ \frac{1}{3}-k_xs_i-a_sx_s \in I \to \frac{1}{3}-k_xs_i-a_sx_s \leq 0\)

    加入这个条件到原问题中，得到解，否则重复上述过程。

    所以，对更接近x.5的变量$x_i$进行分析，得到的解一定是整数解。

    Lecture 14: Stochastic Programming

• Previous
  matlab tutorial
• Next
  判断质数汇编程序编写